[Information Theory] Cross Entropy

본 포스팅은 information theory의 cross entropy 파트를 다루고 있는 posting입니다.

• Cross Entropy

Cross Entropy에 대하여 설명하기 앞서 Shannon entropy를 보고 오는 것을 추천합니다.

Cross Entropy

Cross entropy는 머신러닝과 딥러닝에서 주로 사용되는 loss function 중 하나이다. 이 함수는 모델이 예측한 확률 분포와 실제 데이터의 확률 분포 사이의 차이를 측정한다.

우선 cross entropy를 들어가기 엔트로피를 구하는 식을 알아보자. 엔트로피를 구하는 식은 다음과 같다. 이에 관한 자세한 설명은 다음 링크를 참조하자. \[H(x) = -\sum_x P(x)logP(x) = \sum_x P(x){1 \over logP(x)}\]

총 4개의 item A, B, C, D가 있을 때 이들이 나올 확률 분포 P와 Q가 있다고 가정하자.

Q = [0.25, 0.25, 0.25, 0.25]

P = [0.125, 0.125, 0.25, 0.5]

이 때 확률분포 Q를 P대신 사용할 경우 엔트로피의 변화량을 구하고 싶을 경우 다음과 같은 식을 사용한다.

여기서 우리가 유념해둘 것은 Q를 P대신 사용했으므로 정보량은 Q에 해당하는 것을 사용한다. 그러나 그 정보량이 나올 확률은 변하지 않으므로 정보량의 기대값 즉 entropy는 위 식과 같이 구하는 것이다. 이제 위 식을 일반화하여 적어보면 다음과 같다. \[H(P, Q) = E_{X \sim P}[-logQ(x)] = -\sum_x P(x)logQ(x) \newline\]

보통 머신러닝의 경우 P가 ground truth가 되고 Q가 현재 학습한 확률값이다. 그리고 우리가 학습한 확률값 Q가 P에 가까워질수록 cross entropy의 값은 작아지게 된다. 따라서 loss 값을 줄이려는 머신러닝의 특성상 cross entropy를 loss function으로 사용하면 학습이 성공적으로 진행될 수 있는 것이다.

이해를 돕기위해 수식을 다시 정리하면 다음과 같다. 위에 수식은 𝑃의 정보량을 구하는 수식이고 아래 수식은 cross entropy를 구하는 수식이다.

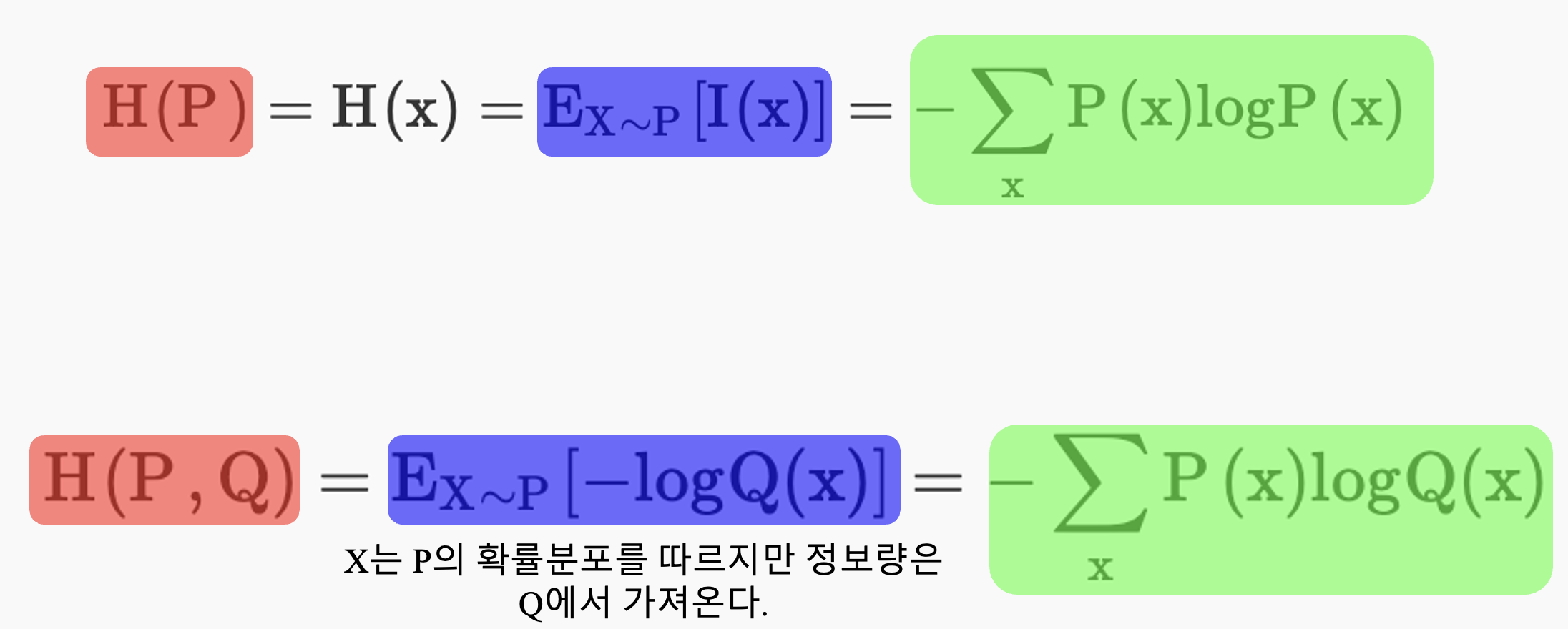
즉 Cross entropy는 실제 확률 분포 𝑃를 따르는 이벤트 𝑋의 정보량을 다른 확률 분포 𝑄를 사용하여 표현할 때의 기대되는 정보량을 측정한다. 간단히 말해, 𝑃는 실제 데이터의 분포를 나타내고, 𝑄는 모델이 예측한 분포이다. Cross entropy는 이 두 분포 사이의 불일치를 수치로 나타내는 것이다.