Information Theory
본 포스팅은 information theory의 기초적인 부분을 다루고 있는 posting입니다.
Shannon entropy
정보량은 불확실성이 커질수록 커진다. 여기서 불확실성이 크다는 말은 곧 사건이 발생할 확률이 적다는 것이다. 예를 들어 “내일은 해가 동쪽에서 뜰 것이다”라는 문장의 정보량은 0에 근사한다. 반면 “내일 비가 올 것이다”라는 문장의 정보량은 비교적 높다. 즉 정리하면 정보량은 다음 3가지 조건을 만족한다.
자주 발생하는 사건은 낮은 정보량을 가진다(100퍼센트 발생하는 사건의 경우 전혀 정보가 없다고 볼 수 있다.)
자주 발생하지 않는 사건의 경우 높은 정보량을 갖는다.
독립 사건은 추가적인 정보량을 갖는다. 즉 동전을 던져 앞면이 두번 나오는 사건에 대한 정보량은 앞면이 한번 나온 정보량의 2배이다.
따라서 정보량은 다음 수식과 같이 구한다. \[I(x) = -logP(x)\]
예를 들어보자. 동전을 던지는 사건과 주사위를 던지는 사건을 비교해보자. 동전의 경우 정보량은 -log20.5 = 1이고 주사위의 경우 -log2(1/6) ≒ 2.5849가 나온다. 즉 주사위의 경우가 동전보다 불확실성이 크므로 정보량도 크게 나온다.
여기서 Shannon entropy는 모든 사건의 정보량의 기대값이다. 즉 전체 사건의 확률 분포의 불확실성을 나타낼 때 사용한다. 어떤 확률분포 P에 대한 Shannon entropy는 다음 수식으로 나타낸다. \[H(P) = H(x) = E_{X \sim P}[I(x)] = E_{X \sim P}[-logP(x)]\]
위 식에 따라 앞면과 뒷면이 나올 확률이 동일한 동전의 경우를 계산해보면 아래와 같다. \[H(P) = H(x) = E_{X \sim P}[I(x)] = -\sum_x P(x)logP(x) \newline = \left(\left(0.5*log0.5\right) + \left(0.5 * log0.5\right)\right) = 1\]
그렇다면 이번에는 N개의 동전을 던졌을 때를 생각해보자. 그러한 경우 수식은 다음과 같다. \[H(P) = H(x) = E_{X \sim P}[I(x)] = -\sum_x P(x)logP(x) \newline = -2^N \left({1 \over 2^N} * log{1 \over 2^N} \right)\]
즉 우리는 위 식을 통해 앞면과 뒷면의 나올 확률이 동일한 동전을 N번 던지는 경우의 불확실성은 N이라는 것을 알 수 있다.
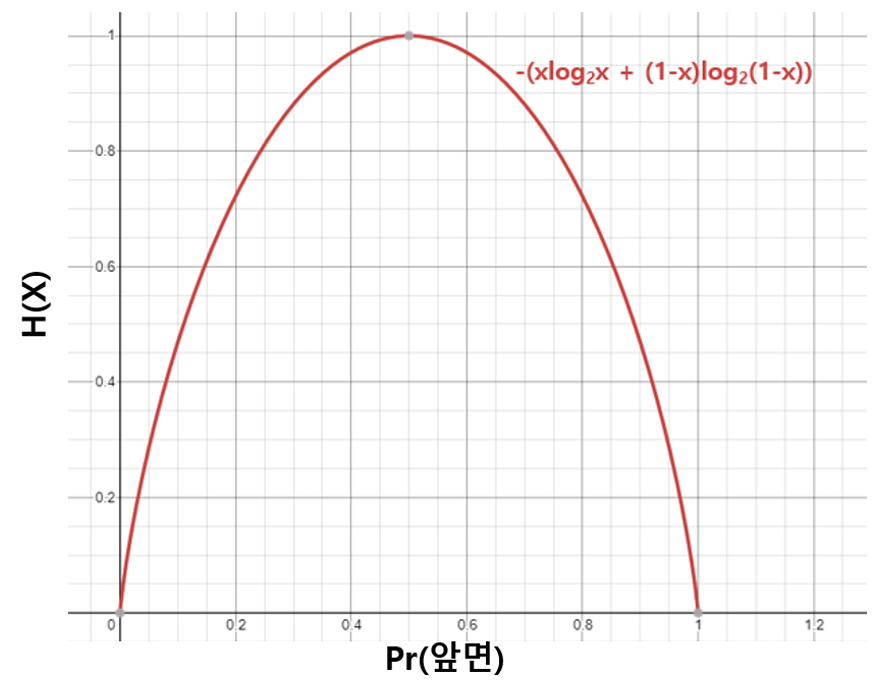
이번에는 동전을 던졌을 때 앞면과 뒷면이 나오는 정도가 동일하지 않다고 해보자. 그 때 앞면이 나올 확률별로 Shannon entropy를 구해보면 다음 그래프와 같다(편의상 동전을 던지는 횟수는 1번이라 가정하자)
Summary
경우의 수가 많다 ⇒ 예측이 어렵다 ⇒ 불확실 성이 크다 ⇒ 어떠한 값이 주어지면 그것에 대한 정보량은 크다
EX)
동전을 던지는 경우(앞, 뒷면이 나올 확률이 같다고 가정)
경우의 수는 2다. ⇒ 예측이 비교적 쉽다 ⇒ 불확실 성이 적다 ⇒ 동전이 앞면이 나왔다는 정보는 정보량이 비교적 적다
주사위를 던지는 경우(모든 눈이 나올 확률이 같다고 가정)
경우의 수는 6이다. ⇒ 예측이 비교적 어렵다 ⇒ 불확실성이 크다 ⇒ 주사위의 눈이 1이 나왔다는 정보는 정보량이 비교적 크다.
참조 링크 : https://ratsgo.github.io/statistics/2017/09/22/information/
