PyIF: A Fast and Light Weight Implementation to Estimate Bivariate Transfer Entropy for Big Data
PyIF는 Kraskov의 방법을 사용하여 이변량 전송 엔트로피를 추정하는 빠른 오픈 소스 Python 구현을 제공하여 병렬화된 KD-Tree 쿼리 및 CUDA 호환 GPU를 사용하여 계산 속도를 크게 높이고 이전 구현보다 최대 1072배 빠른 성능을 달성하는데 성공함.
PyIF: A Fast and Light Weight Implementation to Estimate Bivariate Transfer Entropy for Big Data
Abstract
Transfer entropy는 시간에 따라 변화하는 process간의 정보의 흐름을 정량화 하는 정보 측정이다. Transfer entropy는 금융시장, 표준 시스템, 신경 과학 및 소셜미디어에서 다양하게 쓰인다. 본 논문은 Kraskov의 방법으로 Transfer Entropy를 추정하는 PyIF라는 빠른 open source python 구현을 제공한다. PyIF는 해당 KD-Tree에 대한 쿼리를 병렬화 하여 여러 프로세스 인 KD-Tree를 활용하고 CUDA 호환 GPU와 함께 사용하여 전송 엔트로피를 구하는 시간을 크게 줄일 수 있었다. 분석 결과, PyIF의 GPU 구현이 기존 구현보다 최대 1072 배 더 빠르다(CPU 구현이 181 배 더 빨라짐).
Introduction
상호 정보는 information theory에서 랜덤 변수 간에 공유되는 정보의 양을 정량화 하는 또 다른 척도이다. 상호 정보와 유사하지만 전송 엔트로피 (TE)는 정보의 역학과 이러한 역학이 시간에 따라 어떻게 진화하는지 고려한다. 간단히 말해서, TE는 다른 임의 프로세스의 과거 정보를 알 때 하나의 임의 프로세스에서 불확실성의 감소를 정량화 한다. TE는 또한 정보 전송의 비대칭 척도입니다. 프로세스 A에서 프로세스 B로 계산된 TE와 B에서 A로 계산된 TE는 다른 결과를 산출 할 수 있다.
A. Applications of Transfer Entropy
Network Inference은 TE의 또 다른 응용 분야다. Network Inference의 목적은 데이터에서 개별 프로세스 간의 관계를 식별하여 네트워크를 추론하는 것이다. computational neuroscience(컴퓨팅 신경 과학), 금융 시장 분석, 유전자 규제 네트워크, 소셜 미디어 및 다중 에이전트 시스템은 TE가 네트워크를 모델링하는 데 사용된 영역이다. Network Inference에 TE를 사용한 초기 접근 방식은 네트워크의 모든 변수 쌍 사이에서 pairwise TE를 측정하거나 TE 값을 임계 값으로 설정하여 네트워크에서 노드 간의 연결을 선택한다. 최근 접근법은 링크가 존재하는지 여부를 결정하기 위해 pairwise TE의 통계적 유의성 테스트를 사용했다. 다음 논문은 더 많은 TE 응용 사례를 제공하고 있다(Introduction to Transfer Entropy: Information Flow in Complex).
B. Outline
본 논문은 bivariate TE를 추정하기 위해 제안된 PyIF에 대하여 소개한다. 그리고 이를 기존 구현과 비교 분석을 한 후 마지막으로 discussion과 향후 작업으로 논문을 마무리한다.
Definition Of Transfer Entropy
2000 년에 Schreiber [2]는 TE를 발견하고 “transfer entropy”라는 이름을 만들었지 만 Milian Palus [3]도 독립적으로 개념을 발견했다. 함수 I가 두 확률 분포 사이의 상호 정보를 나타낸다. 지연된 상호 정보 I(X_t : Y_{t-k})는 Y에서 X로의 정보 전송에 대한 time-asymmetric 척도로 사용될 수 있다. 여기서 X와 Y는 모두 임의 프로세스이고 k는 지연 시간이며 t는 현재 기간이다. 그러나 지연된 상호정보는 프로세스 X와 Y간의 shared history(공유 이력)을 설명하지 않기 때문에 충분하지 않다.
TE는 조건부 상호 정보를 통해 두 프로세스 간의 공유 이력을 고려한다. 특히, TE는 X~t~와 과거 사이에 중복되거나 공유된 정보를 제거하기 위해 X~t~의 과거를 조건으로 한다. 이것은 또한 X의 시간 t에대한 X안의 모든 Y의 정보를 제거한다. 따라서 Transfer entropy T(Y에서 X로 정보 전송이 발생하는 경우)는 다음과 같이 정의할 수 있다(X~t-k~가 주어진 상태에서 Y에서 X로의 정보전송의 정보량).
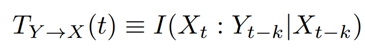
Kraskov는 Transfer entropy가 두 조건부 상호 정보 계산의 차이로 표현될 수 있음을 보여준다.
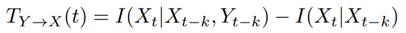
이 정의의 직관은 TE가 X~t~에 대한 X~t-k~의 정보를 고려한 후 X~t~에 대한 Y~t-k~의 정보량을 측정한다는 것이다. 다르게 말하면, TE는 X~t-k~를 알 때 X~t~에 대한 불확실성의 감소를 고려한 후 Y~t-k~를 알 때 X~t~에 대한 불확실성의 감소를 정량화 한다.
Estimating Transfer Entropy
상호 정보를 추정하는 많은 기술이 있습니다. 지금부터 이러한 상호 정보를 추정하기 위한 수식에 대해 알아보고자 한다.
A. Kernel Density Estimator
Kernel Density Estimators는 TE를 추정하는 데 사용할 수 있다. 변수 X 및 Y가있는 크기 n의 bivariate 데이터 세트의 경우 상호 정보는 다음과 같이 추정할 수 있다.
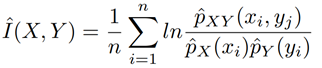
여기서 \(\^{p}_X(x_i)\)및 \(\^{p}_Y(y_i)\)는 추정된 marginal probability density function이고 \(\^{p}_{XY}(x_i, y_j)\)는 joint estimated probability density estimation입니다. x~1~, x~2~, …, x~n~을 포함하는 bivariate 데이터 세트의 경우 각 x가 d 차원 공간에 있는 경우 커널 K를 사용하는 bivariate 커널 밀도 추정기는 다음과 같이 정의된다.
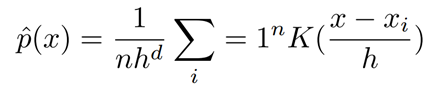
위 식에서 h는 smoothing parameter이고 K는 아래 식으로 정의된다.
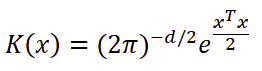
B. Kernel Density Estimator
Transfer Entropy는 k-nearest neighbors을 사용하여 추정할 수 있다.
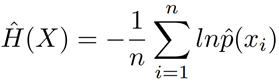
Kraskov이 정의를 확장하여 엔트로피를 다음과 같이 구한다.
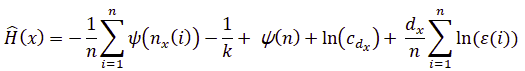
여기서 n은 데이터 포인트의 수, k는 nearest neighbors, \(d_x\)는 \(x\)의 차원, \(c_{d_x}\)는 \(d_x - dimensional unit ball\)의 부피이다. 두 개의 랜덤 변수 X와 Y에 대해 \({\epsilon (i)}\over{2}\)는 \((x_i, y_i)\)사이의 거리이고 k 번째 neighbor는 \((k_{xi}, k_{yi})\)로 표시된다. \({\epsilon_x (i)}\over{2}\)와 \({\epsilon_y (i)}\over{2}\)는 각각 \(\| x_i - kx_i \|\)와 \(\| y_i - ky_i \|\)로 정의된다. \(n_x(i)\)는 \(\| x_i - kx_i \| \leq {\epsilon_x(i)}\over{2}\)와 같은 \(x_j\)의 수이다. \(\psi(x)\)는 아래와 같은 digamma function이다.
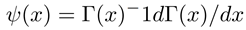
Γ(x)는 일반적인 gamma function이다. 마지막으로 C = 0.5772156649에서 ψ(1) = −C이고 이는 Euler-Mascheroni 상수이다. 랜덤 변수 Y의 엔트로피를 추정하기 위해 Y를 \(\^H(x)\)로 대체할 수 있다.
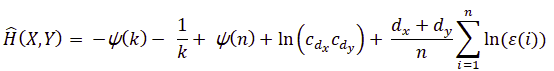
X와 Y 사이의 Joint entropy는 다음과 같이 구할 수 있다.
여기서 \(d_y\)는 \(y\)의 차원이고 \(n_y(i)\)는 \(\vert y_i - y_j \vert \leq {\epsilon_y(i)}\over{2}\)를 만족하는 points \(y_j\)의 수이다. 이 방법을 kraskov estimator라고 한다.
C. Additional Estimators
Khan 또한 상호 정보를 추정하는 데 사용할 수 있는 joint probability density를 추정하기 위해 상호 정보를 계산하고 XY-plane의 adaptive partitioning을 계산하기 위한 differential entropy의 근사 가치가 있는 Edge worth approximation의 유용성을 탐구했다.
궁극적으로 Khan KDE estimator와 Kraskov estimator가 랜덤 프로세스의 종속 구조를 포착하는 능력과 관련하여 다른 방법을 능가한다는 것을 발견했다. 현재 우리 소프트웨어는 Kraskov estimator를 사용하여 bivariate TE estimating을 지원하며 향후 다른 estimator를 추가할 계획이다.
