Taylor Series(테일러 급수)
Taylor Series(테일러 급수)에 대한 간단한 설명을 진행하는 포스팅입니다.
간단한 설명
Taylor series(테일러 급수) 또는 Taylor expansion(테일러 전개)은 우리가 모르는 함수 f(x)에 근사하는 식을 만드는 것이다.
Taylor Series의 수식은 다음과 같다.
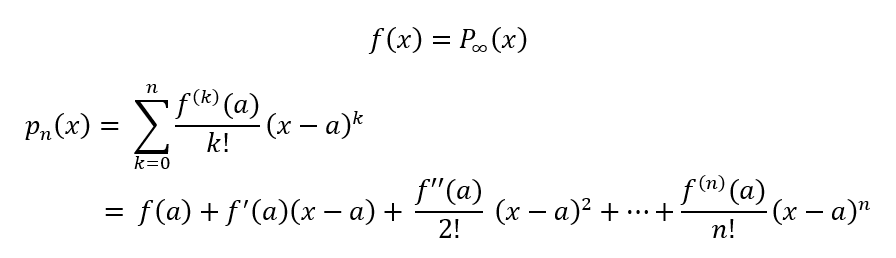
위 식은 일반적인 다차 방정식의 경우 어느 점에서나 성립하지만 삼각함수나 지수 함수의 경우 그렇지 않다.
Taylor serires는 \(x=a\)에서 \(f(x) = p(x)\)이다. 그리고 \(x=a\) 뿐만 아니라 이와 비슷 한 구간에서도 일치한다.
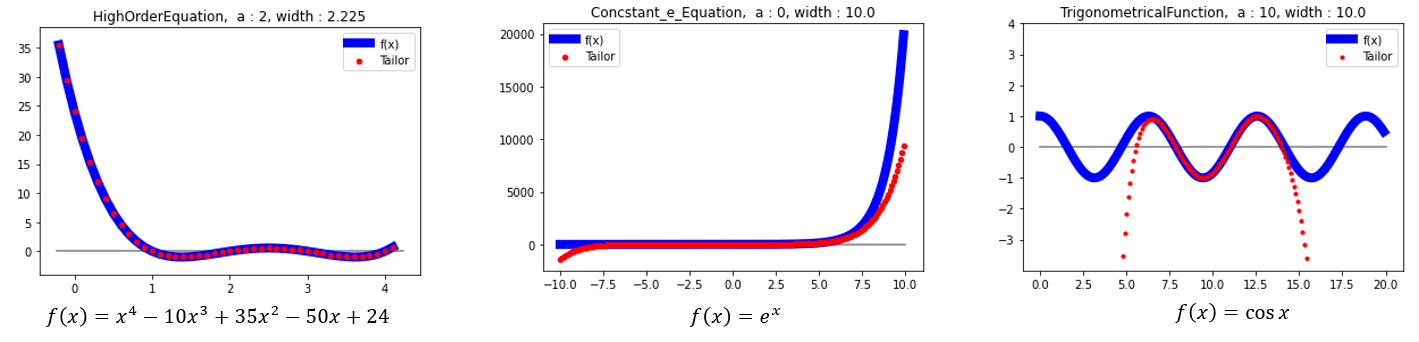
간혹 경우에 따라 f(x)를 1차 또는 2차까지만 테일러 전개하는 경우도 많다. 차수가 커질수록 f(x)와 p(x)간의 차이가 적어진다. 위 그림은 10차까지 전개한것인데 만일 50차까지 전개한다면 다음과 같다.
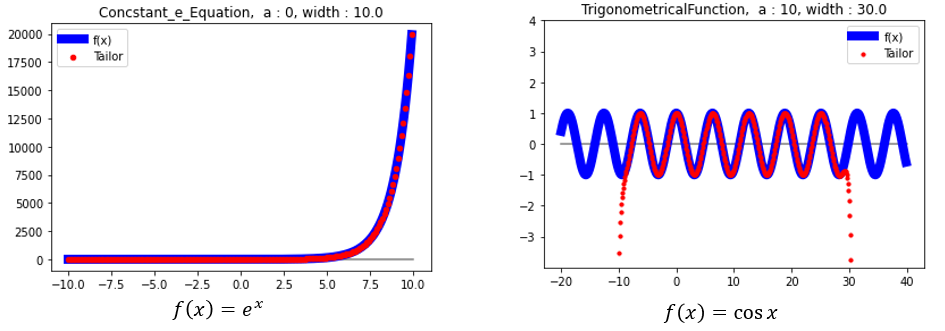
즉 전개하면 전개할수록 점점 더 정확한 값을 얻을 수 있다.
