Quantization의 방법론
본 포스팅은 quantization의 방법론에 대해 소개하고 있습니다.
Quantization에는 여러가지 방법론들이 있습니다. 해당 포스팅은 그러한 방법론의 대표적인 카테고리에 대한 설명을 진행하겠습니다.
Uniform vs Non-Uniform
Quantization은 대표적으로 uniform quantization과 non-uniform quantization으로 나눌 수 있습니다. Uniform quantization은 데이터를 균등한 간격으로 나누는 것이고 non-uniform quantization은 데이터의 분포를 고려하여 비 균등하게 구간을 나누는 방법입니다.
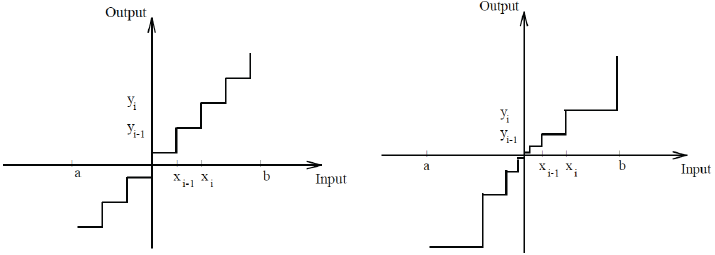
Uniform Distiribution
Uniform Quantization은 데이터를 균등한 간격으로 나누는 방법입니다. 구체적으로는 데이터의 최솟값과 최댓값을 기준으로 일정한 간격으로 분할합니다. Uniform distribution의 특징에는 다음과 같은 것들이 있습니다.
- 적응성: 데이터의 분포에 따라 양자화 구간을 조정할 수 있습니다.
- 효율성: 데이터가 비균등하게 분포된 경우, 특히 피크와 낮은 밀도 영역에서 효율적입니다.
- 복잡성: 구간을 나누는 기준이 복잡하며, 구현이 다소 어려울 수 있습니다.
- 정보 유지: 중요한 데이터 구간에 더 많은 레벨을 할당하여 정보 손실을 줄입니다.
Uniform distribution을 수식적으로 표현하면 다음과 같습니다. \[q_i = \left\lfloor \frac{x - x_{\min}}{\Delta} \right\rfloor \times \Delta + x_{\min}\]
위 수식에서 \(\left\lfloor \ \right\rfloor\)는 내림 표시입니다. 그리고 \(\delta = {x_{max} - x_{min} \over L}\)이고 \(L\)은 양자화 레벨의 수입니다.
Non-Uniform Distiribution
Non-Uniform Quantization은 데이터의 분포를 고려하여 비균등하게 구간을 나누는 방법입니다. 이는 데이터의 밀도가 높은 부분에 더 많은 양자화 레벨을 할당하여, 정보 손실을 최소화하려는 목적을 가집니다. Non-Uniform distribution의 특징은 다음과 같은 것들이 있습니다.
특징
- 적응성: 데이터의 분포에 따라 양자화 구간을 조정할 수 있습니다.
- 효율성: 데이터가 비균등하게 분포된 경우, 특히 피크와 낮은 밀도 영역에서 효율적입니다.
- 복잡성: 구간을 나누는 기준이 복잡하며, 구현이 다소 어려울 수 있습니다.
- 정보 유지: 중요한 데이터 구간에 더 많은 레벨을 할당하여 정보 손실을 줄입니다.
Non-Uniform Quantization에서, 대표적인 방법 중 하나는 Lloyd-Max 알고리즘을 사용하는 것입니다. 이 알고리즘은 양자화 오류를 최소화하는 구간 경계를 반복적으로 계산합니다. 정리하자면 다음과 같습니다.
초기 구간 경계 설정: 먼저, 초기 구간 경계 \(\{b_i\}\)를 설정합니다. 예를 들어, 데이터를 \(L\)개의 구간으로 나눌 때, 초기 구간 경계는 다음과 같이 설정될 수 있습니다: \[b_0 = x_{\min}, \quad b_L = x_{\max}\]
나머지 경계 \(b_1, b_2, \ldots, b_{L-1}\)은 균등하게 나누거나 다른 방식으로 초기화할 수 있습니다.
각 구간에 대한 중심값(대표값) 계산: 각 구간 \(i $에 대한 중심값\)c_i $$는 해당 구간에 속하는 데이터의 평균값으로 계산됩니다: \[c_i = \frac{\int_{b_{i}}^{b_{i+1}} x p(x) \, dx}{\int_{b_{i}}^{b_{i+1}} p(x) \, dx}\]
여기서 \(p(x)\)는 데이터의 확률 밀도 함수입니다.
구간 경계 업데이트: 새로운 구간 경계 \(b_i\)는 인접한 두 중심값의 중간 지점으로 업데이트됩니다: \[b_i = \frac{c_{i-1} + c_i}{2} \quad \text{for} \quad i = 1, 2, \ldots, L-1\]
반복: 위의 2단계와 3단계를 중심값 \(c_i\)와 구간 경계 \(b_i\)가 수렴할 때까지 반복합니다. 즉, 더 이상 큰 변화가 없을 때까지 반복합니다.
Post-Training Quantization
Post-Training Quantization(PTQ)은 학습이 완료된 모델을 quantization하는 방법입니다. 이는 모델을 훈련한 후에 quantization을 적용하므로, 추가적인 훈련 없이 모델을 경량화할 수 있습니다. PTQ는 특히 리소스가 제한된 환경에서 모델을 배포할 때 유용합니다.
Quantization 파라미터
PTQ에서는 두 가지 주요 매개변수인 scale(스케일)과 zero-point(제로 포인트)를 사용하여 부동 소수점 값을 정수로 변환합니다. 이 매개변수들은 다음과 같이 정의됩니다:
- Scale: 입력 값의 범위를 양자화된 정수 범위에 맞추는 비율.
- Zero-point: 정수 0이 대응하는 부동 소수점 값.
Quantization 과정
PTQ의 주요 과정은 다음과 같습니다.
- Calibration: 훈련된 모델의 일부 입력 데이터(교정 데이터)를 사용하여 각 layer의 activation range를 측정합니다. 이를 통해 scale과 zero-point를 결정합니다. 예를 들어, 입력 데이터 \(x\)가 \([x_{\min}, x_{\max}]\)범위에 있다고 가정할 때, scale과 zero-point는 다음과 같이 계산됩니다(여기서 \(b\)는 양자화 비트 수(예: 8 bit)입니다):
- Quantization: 각 층의 가중치와 활성화 값을 8비트 정수로 변환합니다. 이를 위해, 가중치와 활성화 값을 정수로 변환합니다. 정수 변환 과정은 다음과 같습니다.
- Inference: 양자화된 모델을 사용하여 추론을 수행합니다. 이 때 필요 시, 정수 값을 다시 부동 소수점 값으로 변환하여 최종 출력을 얻습니다.
장단점
장점:
- 메모리 절약: 32비트 부동 소수점 값을 8비트 정수로 변환하여 모델 크기를 줄입니다.
- 연산 속도 향상: 정수 연산이 부동 소수점 연산보다 빠르기 때문에 추론 속도가 빨라집니다.
- 배포 용이성: 경량화된 모델을 모바일 장치나 임베디드 시스템에 쉽게 배포할 수 있습니다.
단점:
- 정밀도 손실: 양자화 과정에서 일부 정보 손실이 발생할 수 있어 모델의 정확도가 약간 감소할 수 있습니다.
- 복잡한 교정 과정: 교정 데이터가 필요한데, 이는 양자화 과정에서 추가적인 복잡성을 초래할 수 있습니다.
예시
간단한 예시로, ResNet과 같은 복잡한 신경망 모델을 생각해봅시다. ResNet 모델을 훈련한 후 PTQ를 적용하려면 다음 단계를 따릅니다:
- 훈련된 모델 준비: 사전 훈련된 ResNet 모델을 준비합니다.
- 교정 데이터 선택: 모델의 교정에 사용할 일부 입력 데이터를 선택합니다.
- Calibration 수행: 교정 데이터를 사용하여 각 층의 활성화 범위를 측정하고 scale과 zero-point를 계산합니다.
- 양자화 변환: ResNet 모델의 모든 가중치와 활성화 값을 8비트 정수로 변환합니다.
- 양자화된 모델 추론: 양자화된 모델을 사용하여 추론을 수행하고, 성능을 평가합니다.
이 과정은 TensorFlow Lite, PyTorch Quantization Toolkit 등과 같은 도구를 사용하여 쉽게 수행할 수 있습니다.
Quantization Aware Training
Quantization-Aware Training(QAT)은 모델을 훈련하는 동안 양자화를 고려하는 방법입니다. 이는 모델의 훈련 과정에서 quantization의 영향을 반영하여, 최종적으로 양자화된 모델의 성능을 최적화하는 데 중점을 둡니다. QAT는 양자화로 인한 정확도 손실을 최소화하기 위해 훈련 중에 양자화된 가중치와 활성화를 사용합니다.
주요 개념
훈련 중 양자화 시뮬레이션: QAT는 훈련 과정에서 양자화된 가중치와 활성화를 시뮬레이션합니다. 이는 모델이 양자화로 인한 오류를 학습하고 보정할 수 있게 합니다.
가중치와 활성화의 양자화: QAT는 각 훈련 단계에서 가중치와 활성화를 양자화합니다. 이를 통해, 양자화된 모델의 추론 시나리오를 훈련 동안에 반영할 수 있습니다.
그래디언트 업데이트: 양자화된 가중치와 활성화로 인해 발생하는 그래디언트 변화를 고려하여, 최적화 알고리즘이 업데이트됩니다. 이는 모델이 양자화로 인한 손실을 최소화할 수 있게 합니다.
QAT 절차
- 초기 모델 준비:
- 사전 훈련된 모델을 준비하거나 초기화된 모델로 시작합니다.
- 모델의 가중치와 활성화 값을 8비트 정수로 양자화합니다.
- 양자화 매개변수 설정:
- 모델의 각 레이어에 대해 scale과 zero-point를 설정합니다.
- 초기 scale과 zero-point는 일반적으로 교정 데이터를 사용하여 계산됩니다.
- 훈련 데이터 사용:
- 표준 훈련 데이터와 손실 함수를 사용하여 모델을 훈련합니다.
- 각 훈련 단계에서 가중치와 활성화를 양자화합니다.
- 양자화된 가중치와 활성화 사용:
- 양자화된 가중치와 활성화를 사용하여 forward pass와 backward pass를 수행합니다.
- 양자화된 값들로 인해 발생하는 손실을 최소화하도록 모델을 최적화합니다.
- 최적화:
- 모델의 손실 함수와 최적화 알고리즘을 사용하여 가중치를 업데이트합니다.
- 양자화로 인한 그래디언트 변화를 고려하여 가중치를 조정합니다.
- 양자화된 모델 생성:
- 훈련이 완료된 후, 최종적으로 양자화된 모델을 생성합니다.
- 이 모델은 8비트 정수로 표현된 가중치와 활성화를 포함합니다.
장단점
장점:
- 정밀도 유지: 훈련 과정에서 양자화의 영향을 반영하여, 양자화로 인한 정확도 손실을 최소화할 수 있습니다.
- 효율적인 배포: QAT로 훈련된 모델은 메모리 사용량과 계산 복잡도가 줄어들어, 모바일 장치나 임베디드 시스템에서 효율적으로 동작합니다.
단점:
- 훈련 시간 증가: 양자화된 가중치와 활성화를 사용하는 추가적인 계산으로 인해 훈련 시간이 늘어날 수 있습니다.
- 복잡성 증가: 훈련 과정에서 양자화의 영향을 시뮬레이션하고 반영해야 하므로, 구현이 복잡해질 수 있습니다.
예시
간단한 예시로, MobileNet과 같은 신경망 모델을 QAT를 사용하여 훈련하는 과정을 생각해봅시다:
- 초기 모델 준비: 사전 훈련된 MobileNet 모델을 준비합니다.
- 양자화 매개변수 설정: 각 레이어에 대해 초기 scale과 zero-point를 설정합니다.
- 훈련 데이터 사용: 표준 훈련 데이터를 사용하여 모델을 훈련합니다.
- 양자화된 가중치와 활성화 사용: 각 훈련 단계에서 양자화된 가중치와 활성화를 사용하여 순전파와 역전파를 수행합니다.
- 최적화: 손실 함수와 최적화 알고리즘을 사용하여 가중치를 업데이트합니다.
- 양자화된 모델 생성: 훈련이 완료된 후, 최종적으로 양자화된 MobileNet 모델을 생성합니다.
결론
Quantization-Aware Training (QAT)은 모델을 훈련하는 동안 양자화를 고려하여, 최종적으로 양자화된 모델의 성능을 최적화하는 방법입니다. 이는 양자화로 인한 정확도 손실을 최소화하며, 리소스가 제한된 환경에서 모델을 효율적으로 배포할 수 있게 합니다.
Q1: QAT와 Post-Training Quantization (PTQ)의 주요 차이점은 무엇인가요?
Q2: QAT를 적용할 때 가장 중요한 고려사항은 무엇인가요?
Q3: QAT를 사용하여 모델을 훈련할 때 발생할 수 있는 문제점은 무엇인가요?
