D-H 파라미터(Denavit-Hartenberg Parameter, DH Parameter)
본 포스팅은 D-H parameter에 대해 간략히 정리하여 소개하고 있습니다.
D-H 파라미터(Denavit-Hartenberg Parameter, DH Parameter)는 로봇의 link와 joint를 수학적으로 표현하여 각 관절의 움직임을 기술하는 데 사용되는 방법론이다. 이 파라미터화 방식은 로봇 매니퓰레이터와 같은 관절 시스템의 기구학적 구조를 간결하게 표현하고 분석하는 데 매우 유용하다.
D-H 파라미터는 4개의 값으로 이루어져 있으며, 이 값들은 두 링크 사이의 상대적인 위치와 회전을 정의합니다. 각 조인트에서 다음 4가지 파라미터가 사용됩니다:
- Link 길이 $a_i$:
- Joint축 $Z_i$와 $Z_{i+1}$ 사이의 거리를 나타냄.
- 두 축이 수직이면 $a_i$는 두 축 사이의 수직 거리이다.
- 이는 링크의 물리적 길이를 나타낼 수 있다.
- Link 각도 $\alpha_i$:
- $Z_i$와 $Z_{i+1}$ 축 사이의 회전 각도.
- 이는 링크가 얼마나 비틀려 있는지를 나타냄.
- 즉, 두 축이 평행하지 않다면, $Z_i$에서 $Z_{i+1}$으로 회전하기 위해 $X$ 축을 따라 회전해야 하는 각도.
- Link offset $d_i$:
- Joint 축 $Z_i$를 따라 링크 간의 거리를 나타냄.
- 이는 링크와 링크 사이의 직선 이동량이다.
- Joint 각도 $\theta_i$:
- 조인트 축 $Z_i$를 기준으로 한 회전 각도.
- 이는 Joint가 얼마나 회전하는지를 나타냄.
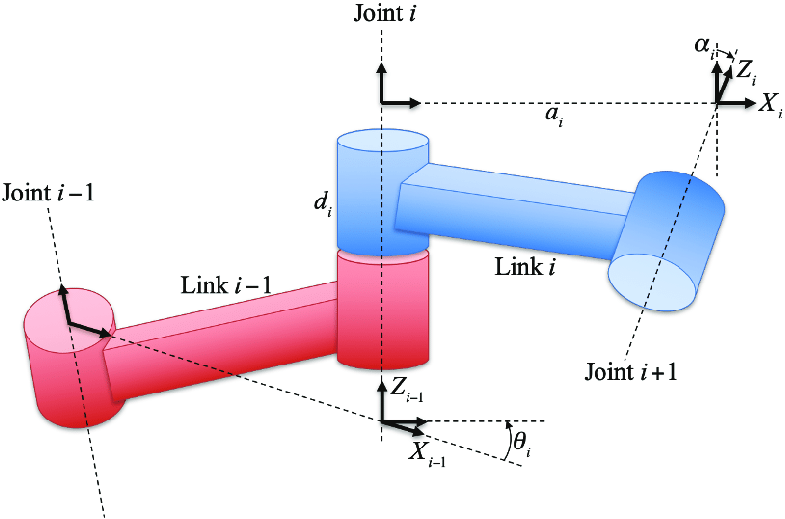
D-H 파라미터 정의 과정
- 축 정의: 각 조인트 축은 $Z$ 방향을 따라 정의됨
- Link 길이와 각도: 각 링크 사이의 $X$축을 기준으로, 링크 길이와 링크 각도를 정의.
- 변환 행렬 계산: 변환 행렬은 한 링크 좌표계에서 다음 링크 좌표계로의 변환을 나타내며, 기구학적 계산에 매우 유용하다. 변환 행렬은 각각의 D-H 파라미터는 4x4 변환 행렬을 통해 나타낼 수 있다.
D-H 파리미터 변환 행렬
변환 행렬 $T_i^{i+1}$는 다음과 같이 주어진다. \[T_i^{i+1} = \begin{bmatrix} \cos \theta_i & -\sin \theta_i \cos \alpha_i & \sin \theta_i \sin \alpha_i & a_i \cos \theta_i \\ \sin \theta_i & \cos \theta_i \cos \alpha_i & -\cos \theta_i \sin \alpha_i & a_i \sin \theta_i \\ 0 & \sin \alpha_i & \cos \alpha_i & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\]
D-H 파라미터의 활용
- 순방향 기구학(Forward Kinematics)
D-H 파라미터를 이용하여 각 조인트의 회전이나 변위를 주었을 때, 로봇의 end-effector의 위치와 자세를 계산할 수 있다.
- 역방향 기구학(Inverse Kinematics)
로봇의 end-effector가 특정한 위치와 자세에 도달하도록, 각 조인트의 값을 계산할 수 있습니다.
