[Information Theory] KLD(Kullback-Leibler Divergence)

본 포스팅은 cross entropy를 알고 있다는 가정하에 KL Divergence에 대한 설명을 진행합니다.

• KLD의 기본 개념
• KLD와 Cross Entropy의 차이

KLD의 기본 개념

KL divergence는 두 확률분포의 차이를 계산하는데 사용되는 함수입니다. 즉 다시말하면 어떠한 이상적인 분포에 대하여 그 분포를 근사하는 다른 분포를 대신 사용하여 샘플링을 진행한다면 발생할 수 있는 정보량의 차이(확률 분포 Q가 확률 분포 P를 얼마나 잘 대치할 수 있는지)를 말하는 것 입니다. 딥러닝 모델을 만들 때를 예로 들면 우리가 가지고 있는 데이터의 분포 P(x)와 모델이 추정한 데이터의 분포 Q(x)간의 차이를 KLD(KL-Divergence)를 활용해 구할 수 있습니다. 이 두 분포의 차이를 시각화하면 다음과 같습니다.

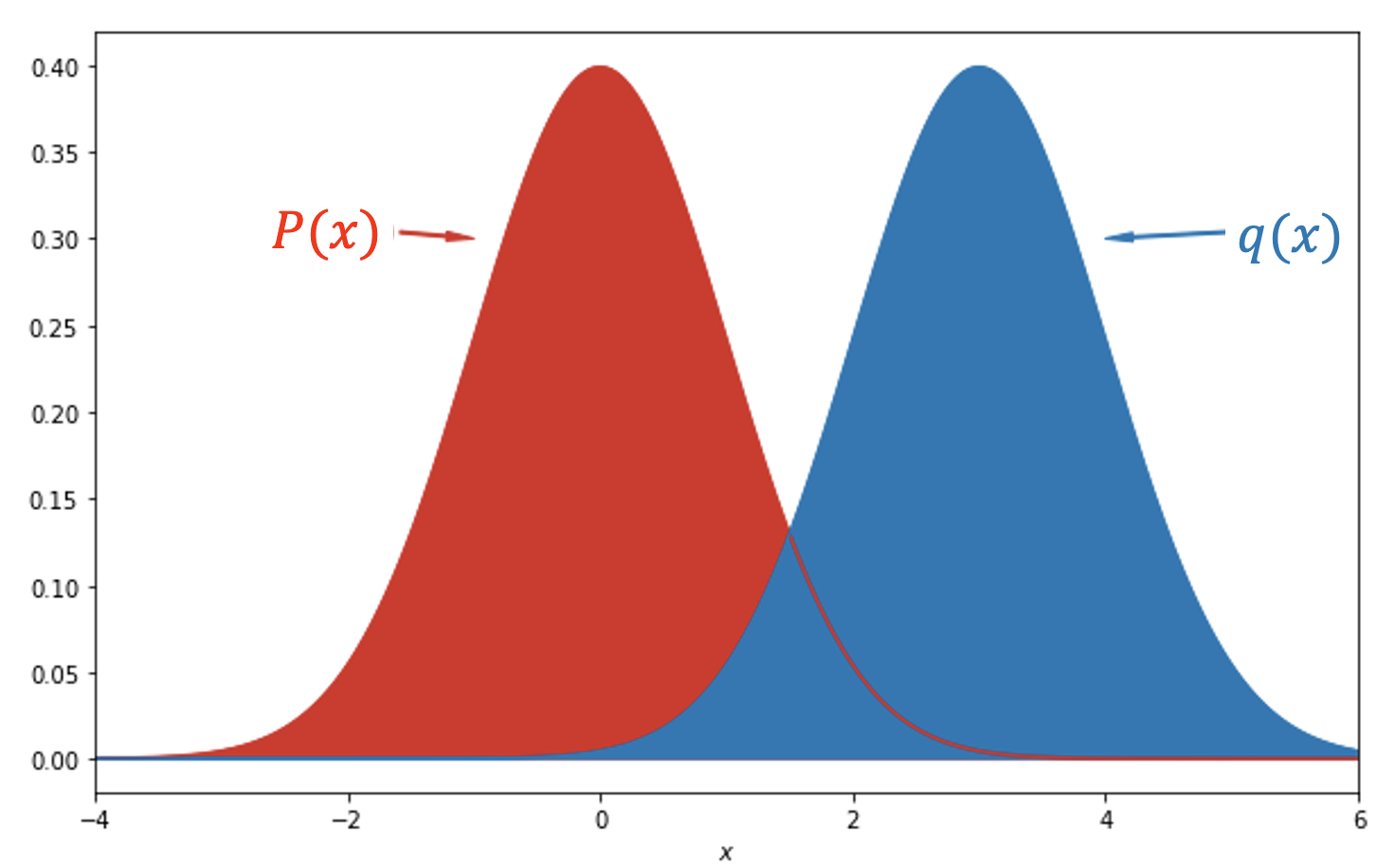
위 그림에서 우리는 Q가 P를 얼마나 잘 나타내는지를 알기 위해 두 분포간의 차를 구해야 합니다(이 때 정의역, 즉 x는 P로부터 sampling 됩니다). 따라서 KLD의 식은 다음과 같이 쓸 수 있습니다. \[\begin{aligned} %!!15 D_{KL}(P||Q) = E_{X \sim P}\left[log{P(x) \over Q(x)}\right] &= E_{X \sim P}\left[log{P(x)}\right] + E_{X \sim P}\left[-log{Q(x)}\right] \\[2em] &= -H(P) + H(P, Q) \end{aligned}\]

즉 KLD는 엔트로피와 실제 확률분포 P의 차이로 구할 수 있습니다. 이 때 만일 두 확률분포가 동일할 경우 KLD의 값은 0이 됩니다. 단 KLD는 비대칭으로 P와 Q의 위치가 바뀌면 KLD의 값도 바뀝니다. 즉 KLD를 거리함수라고 보면 안 됩니다.

지금부터 위 수식에 대하여 자세히 알아보겠습니다. 위에서 KLD는 두 확률분포의 차이를 계산한다고 했는데 조금 더 정확히 말하면 KLD는 어떠한 확률 분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P대신 사용할 경우 엔트로피의 변화를 의미합니다. 따라서 우리는 식을 다음과 같이 고쳐 쓸 수 있습니다.

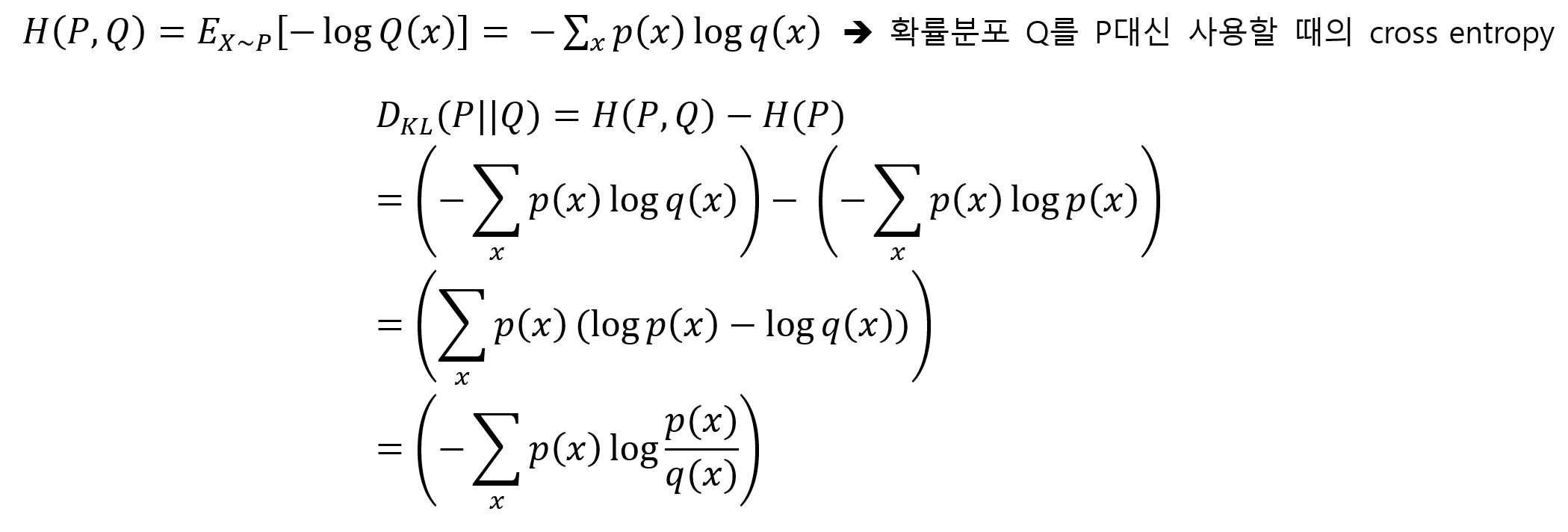
따라서 우리는 위 식을 통하여 두 확률 분포의 차이를 계산할 수 있습니다.

KLD와 Cross Entropy의 차이

Cross entropy는 실제 데이터 분포 𝑃에 대하여 모델이 예측한 분포 Q가 얼마나 일치하는지를 측정한다. 반면 KLD는 𝑃를 사용하여 얻을 수 있는 정보 대비 Q를 사용했을 때 필요한 추가 정보량을 나타낸다.

	KLD	Cross Entropy
목적	𝑃를 사용하여 얻을 수 있는 정보 대비 𝑄를 사용했을 때 필요한 추가 정보량	모델이 예측한 분포 Q가 𝑃와 얼마나 일치하는지
기능	Q가 𝑃를 얼마나 잘 대체할 수 있는지를 수치화	𝑄가 𝑃를 얼마나 잘 표현하는지를 수치화