[Information Theory] Transfer Entropy
본 포스팅은 Information Theory, cross entropy, KL-divergence를 알고 있다는 가정하에 Transfer Entropy에 대한 간략한 설명을 진행합니다.
Transfer Entropy의 정의
Transfer Entropy는 두 객체의 인과관계의 정도를 알아보기 위하여 도입된 개념이다. 즉 Transfer entropy에서는 시간의 개념이 포함되어 있다.
만약 X의 행동이 Y로부터 유발된 것이라고 추측한다면 X의 현재 행동은 Y의 행동과 상관관계가 존재하야 한다. 즉 \(x_t\)는 \(y_{t-1}, y_{t-2} ...\)와 상관관계가 존재해야 한다는 것이다.
이 말은 X의 이전 data만 주어졌을 때와 여기에 Y의 data가 추가로 주어졌을 때 불확실성(entropy)이 변한다는 것이고 이 차이가 클수록 \(x_{t}\) 는 Y의 이전 값들에 의해 영향을 크게 받는다는 것이다.
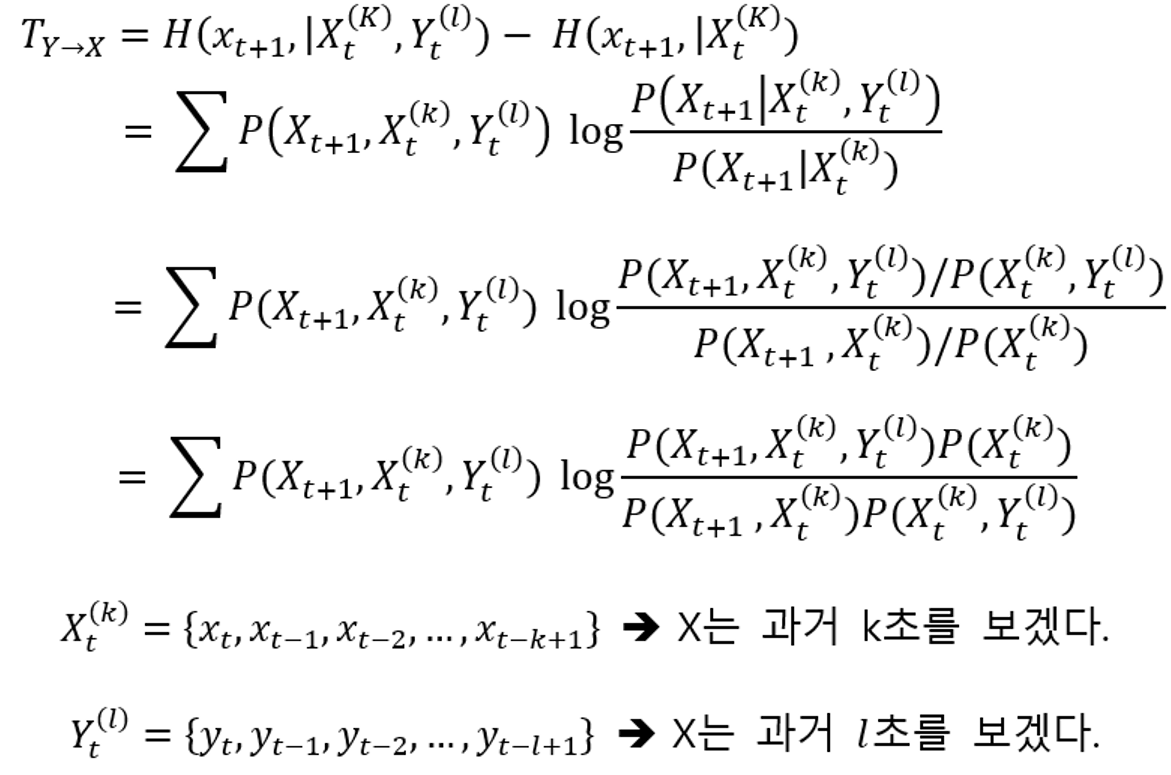
위 식을 다시 설명하면 \(X_t^{(k)}\)가 주어졌을 때 \(x_{t+1}\)이 갖는 정보량과 \(X_t^{(k)}\)와 \(Y_t^{(l)}\)이 주어졌을 때 \(x_{t+1}\)이 갖는 정보량의 차이를 구하겠다는 식이다. 만약 이 값의 차이가 크다면 \(Y_t^{(l)}\)이 \(x_{t+1}\)에 미치는 영향이 크다고 봐도 될 것이다.
Example
극단적으로 말해서 만일 \(H(x_{t+1} | X_t^{(k)}) = 0.1\)이지만 \(H(x_{t+1} | X_t^{(k)}, Y_t^{(l)}) = 1.0\)이라면 \(x_{t+1}\)은 \(Y_t^{(l)}\)이 주어져야 비로소 확정되고 이는 곧 \(Y_t^{(l)}\)은 \(x_{t+1}\)에 많은 영향을 끼친다는 것이다.
TE에 대하여 더 자세히 알고 싶다면 다음 링크를 참조하자.
https://myunghaklee.github.io/blog/paper/2021-03-25-PyIF/
참조 링크
https://mons1220.tistory.com/154
https://ikegwu.com/assets/papers/2020_Ikegwu_Traguer_McMullin_Brunner_05FA.pdf
